Outline

1. Overview
2. Pseudonyms for VCs
3. Hidden PID Pseudonyms
4. Anonymous Holder Binding

Me and My VC Work

* W3C “Invited Expert”, semi-retired, website: Grotto Networking

• Helping (co-editor) with: VC-DI, VC-DI-EdDSA, VC-DI-ECDSA, VC-DI-BBS specs
• Cryptographic test vector generation for the specs EdDSA and ECDSA and ECDSA-SD and BBS (open source code)
• Open Source implementations: VC-DI-ECDSA-SD, BBS Scheme (IETF), VC-DI-BBS, VC-Server (tiny implementation for interoperability testing)
• Helping out with IETF BBS specs: BBS, Blind BBS, BBS per Verifier Id (pseudonym).

Tracking

Every Breath You Take, The Police, 1983

Every breath you take and every move you make

Every bond you break, every step you take,

I’ll be watching you

Frequently mistaken for a love song, really about a stalker

More Realistically

Bloom County November 5, 2009

Tracking with Verifiable Credentials 1

Verifier-Verifier Collusion

Tracking with Verifiable Credentials 2

Verifier-Issuer Collusion

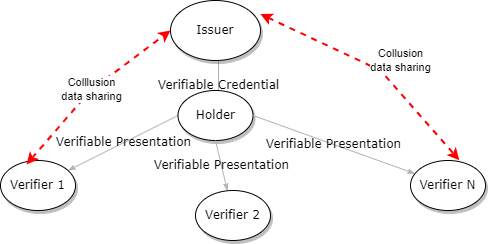
Tracking with Verifiable Credentials 3

Verifier - Third Party Collusion

Anonymity with Verifiable Credentials

See BBS VC Privacy Considerations

• Selective Disclosure: minimize what you reveal to verifiers
• Unlinkable Proofs: make sure security features don’t act as an identifier
• The BBS Signature Scheme applied to VCs can provide both

Tracking in EUDIW 1

From Official Journal of the European Union, April 2024.

16. The technical framework of the European Digital Identity Wallet shall:

• (a) not allow providers of electronic attestations of attributes or any other party, after the issuance of the attestation of attributes, to obtain data that allows transactions or user behaviour to be tracked, linked or correlated, or knowledge of transactions or user behaviour to be otherwise obtained, unless explicitly authorised by the user;

Tracking in EUDIW 2

From Official Journal of the European Union, April 2024.

16. The technical framework of the European Digital Identity Wallet shall:

• (b) enable privacy preserving techniques which ensure unlikeability, where the attestation of attributes does not require the identification of the user.

Less than Complete Anonymity

Don’t You (Forget About Me) by Simple Minds 1985

• Let a verifier associate you with your previous encounters, but not link your data with other verifiers
• Let a verifier associate you with your previous encounters, but not link your data with other verifiers, but allow issuer to know its you. Example: hoarding prevention.

Is this possible?

Pseudonyms

From Wikipedia: Pseudonym

• “A pseudonym or alias is a fictitious name that a person assumes for a particular purpose, which differs from their original or true name. … Many pseudonym holders use them because they wish to remain anonymous…”
• Examples: “Samuel Clemens, writing as Mark Twain, … The British mathematician Charles Dodgson wrote fantasy novels as Lewis Carroll and mathematical treatises under his own name.”

Pseudonyms on the Web

One Approach

• Use a different user name for each web site
• Use a different password for each web site
• Use a unique email address for each web site. Hard but can use Unique Private Duck Addresses

But what if website requires some type of “proof” about you? That is requires information issued and signed by some trusted issuer => a VC

Pseudonyms in EUDIW

From Official Journal of the European Union, April 2024.

4. European Digital Identity Wallets shall enable the user, in a manner that is user-friendly, transparent, and traceable by the user, to:

   • (b) generate pseudonyms and store them encrypted and locally within the European Digital Identity Wallet;

One approach to pseudonyms with a VC

Have an issuer issue a VC to the holder under each pseudonym that the holder wants. Problems:

1. Issuer would need to issue lots of near-duplicate credentials to the holder for each verifier that the holder encounters (let’s solve this first)
2. Issuer knows the holders pseudonyms and can track all their encounters with verifiers

A Cryptographic per Verifier Pseudonym

Create a pseudonym based on holder secret and verifier public data

• Let holder have a “secret” number called a prover identifier (pid), that is essentially unique
• Let verifier have a public essentially unique number called the verifier identifier (vid)
• The holder generates the \(pseudonym = vid^{pid}\) and shares it with the verifier

How does this help?

• Issuer only needs to sign the VC with info about the prover identifier (pid)
• Holder can generate pseudonyms for any verifier that publishes a verifier identifier (vid)
• With appropriate parameters the the difficulty of the discrete logarithm problem prevents any other verifiers discovering the pid from the pseudonym and linking with other verifiers.

PID, VID, and Pseudonym Implementation

• A pid value would be a number, called a scalar in BBS. The BBS scheme has a function to hash an arbitrary byte string into a scalar.
• The vid value would be an element of the group \(\mathbb{G}_1\) in BBS. BBS has a function to hash an arbitrary byte string into such an element.
• The pseudonym value would also be an element of the group \(\mathbb{G}_1\). BBS has functions for encoding and decoding such elements.

Issuer Known PID Flow

Issuer Duties: Known PID Pseudonym

1. Generates an essentially unique pid value.
2. Creates a BBS signature for the VC adding the pid value as the last message in the ordered list of BBS messages.
3. Sends VC with base proof and pid to holder

Holder Duties: Known PID Pseudonym

1. Obtains the verifiers public verifier identifier (vid) value
2. Compute the pseudonym based on pid and vid
3. Determines the minimal amount of info to disclose to the verifier (not the pid)
4. Sends VC with derived proof (enhanced) and pseudonym to verifier

Enhancing BBS Proofs for Pseudonyms

The BBS proof is extended to include a zero-knowledge proof of correctness of the pseudonym value, i.e., that is correctly calculated using the (undisclosed) id of the Prover (pid), and that is “bound” to the underlying BBS signature (i.e., that the pid value is signed by the Signer).

Verifier Duties: Known PID Pseudonym

1. Receives VC with derived proof and pseudonym from holder
2. Uses pseudonym and VC in enhanced BBS proof verification procedure to verify proof and pseudonym.

Hiding the PID from the Issuer

• How can we prevent the issuer from knowing the pid and hence be able to track all the holders encounters with verifiers?

• How could we have the same pid be used by different issuers without revealing it?

• Have the holder generate the pid and keep it secret! Huh?

Holder Commits to a PID

From Wikipedia: Commitment Scheme

A commitment scheme is a cryptographic primitive that allows one to commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later. Commitment schemes are designed so that a party cannot change the value or statement after they have committed to it: that is, commitment schemes are binding.

Commitment Scheme Properties

A Graduate Course in Applied Cryptography, Dan Boneh and Victor Shoup, section 8.12

1. “Binding: Once a commitment c is generated, Alice can only open it to a single message.” => No changing the message/value after the commitment has been made.
2. “Hiding: The commitment string c should reveal no information about the committed message” => this is true even if the message set is under the control of the adversary.

Example: Hash Based Commitment Scheme

1. Let m be the value/message being committed
2. Choose r randomly
3. Compute the commitment \(c = H(m || r)\) where H() is a hash function
4. Send \((c, r)\)
5. Verification on reveal of m by checking \(c = H(m || r)\).

Example: Pedersen Commitment

1. Let g and h be generators of the same (prime) group
2. Let x be a number (message) to be committed
3. Let r be a random number (blinding factor)
4. Compute the commitment as \(c = g^x h^r\)

But if we reveal the pid…

• If we reveal the pid we can be tracked.
• Instead we provide a “proof” that we know the pid
• And require that this “proof” does not reveal any information about the pid
• This is known as a “zero knowledge proof” (ZKP)

ZKP Concepts

From A Graduate Course in Applied Cryptography section 19.5.1

• Correctness: “an interaction between an honest prover and an honest verifier always produces an accepting conversation.”
• Special Soundness: essentially means that the prover must know what they claim to know in order to complete the proof protocol.
• Honest Verifier Zero Knowledge: essentially means that a verifier (not using active attacks) will not learn anything about the unknown information from the proof protocol.

Proving a Pedersen Commitment Setup

• Prover and verifier know \(g, h \in \mathbb{G}\) (generators)
• Prover knows: \(\alpha\) and \(\beta\), computes \(u = g^\alpha h^\beta\)
• Prover gives \(u\) to the verifier and wants to prove they know \(\alpha\) and \(\beta\)

Interactive Proof Overview

From From A Graduate Course in Applied Cryptography

Interactive Proof Procedure

1. The prover selects random values \(\alpha_t\) and \(\beta_t\) and computes \(u_t = g^{\alpha_t} h^{\beta_t}\). This value is sent to the verifier.
2. The verifier selects a random value \(c\) and sends it to the prover.
3. The prover computes \(\alpha_z = \alpha_t + \alpha c\) and \(\beta_z = \beta_t + \beta c\) and sends them to the prover.
4. The verifier checks if \(g^{\alpha_z}h^{\beta_z} = u_t \cdot u^c\). If so the proof is accepted.

Proof of Correctness

See A Graduate Course in Applied Cryptography for special soundness and HVZK.

\[\begin{array}{rcl} g^{\alpha_z}h^{\beta_z} & = & g^{\alpha_t + \alpha c}h^{\beta_t + \beta c} \\ & = & g^{\alpha_t} h^{\beta_t} \cdot (g^\alpha h^\beta)^c \\ & = & u_t \cdot u^c \end{array}\]

Blind Signatures 1

From Wikipedia: Blind Signatures

In cryptography a blind signature is a form of digital signature in which the content of a message is disguised (blinded) before it is signed. The resulting blind signature can be publicly verified against the original, unblinded message in the manner of a regular digital signature.

Blind Signatures 2

From Wikipedia: Blind Signatures

Blind signatures are typically employed in privacy-related protocols where the signer and message author are different parties. Examples include cryptographic election systems and digital cash schemes.

BBS Blind Signatures

From BBS Blind Signatures

The BBS digital signature scheme can be extended to support blind signatures functionality. In a blind signatures setting, the user (called the Prover in the context of the BBS scheme) will request a signature on a list of messages, without revealing those messages to the Signer (who can optionally also include messages of their choosing to the signature).

BBS Blind Signature API

• BlindSign(SK, PK, commitment_with_proof, header, messages, signer_blind), Blind BBS signatures work with a commitment and its proof (from holder).
• messages are from the issuer
• BlindProofGen(PK,signature, header, ph, messages, committed_messages, disclosed_indexes, disclosed_commitment_indexes, secret_prover_blind, signer_blind)

Pseudonym with Hidden PID Flow

Signature Compromise/Impersonation

From BBS Blind Signatures

In the BBS scheme, knowledge of a valid signature allows generation of BBS proofs. As a result, a signature compromise can lead to impersonation of the Prover by malicious actors (especially in cases involving “long-lived” signatures, as in digital credentials applications etc.,).

Note: This is true of any currently secured VC

Locking Down the VC

From BBS Blind Signatures

Using Blind BBS Signatures the Prover can commit to a secret message before issuance, guaranteeing that no one will be able to generate a valid proof without knowledge of their secret.

Note: This does not impact anonymity of holder hence Anonymous Holder Binding

Anonymous Holder Binding Flow

BBS for VC Advanced Feature Recap

• Completely unlinkable Pseudonyms for VCs (Hidden PID Pseudonym)
• Verifier unlinkable Pseudonyms for VC (Issuer Known PID Pseudonym)
• Cryptographically Strong but unlinkable binding of VC to Holder (Anonymous Holder Binding)

Status

• All cryptographic techniques well established and contained in BBS literature.
• All cryptographic techniques already in use in current BBS draft
• Current work to finalize Blind BBS and BBS per Verifier Id (pseudonym) APIs and implementation specifics. Driven by app requirements.