Public Key Cryptography

Dr. Greg Bernstein

October 12th, 2021

Asymmetric Cryptography

References

Big Applications

Wikipedia: TLS, The Transport Layer Security (TLS) Protocol Version 1.3 – the security of the Web rests on public key cryptography.
Wikipedia: SSH, Comparing SSH Keys – A better way to connect to servers is via public key cryptography!
Wikipedia: S/MIME, Secure/Multipurpose Internet Mail Extensions (S/MIME) Version 4.0 Message Specification

The Key Distribution Problem

Securing Communications I

How many symmetric keys are needed for N nodes to communicate?

Securing Communications II

\(N(N-1)/2\) keys

How to Distribute the Keys?

We’ve got a problem…

Need a secure channel to distribute the key
Need a key to create a secure channel
If a key is compromised there is no security

Public Key Cryptography History IA

From Wikipedia: Public Key Cryptography classified history

1970: James H. Ellis, a British cryptographer at the UK Government Communications Headquarters (GCHQ), conceived of the possibility of “non-secret encryption”, (now called public key cryptography), but could see no way to implement it.
1973: Clifford Cocks (GCHQ) implemented what has become known as the RSA encryption algorithm, giving a practical method of “non-secret encryption”,

Public Key Cryptography History IB

From Wikipedia: Public Key Cryptography classified history

1974 another GCHQ mathematician and cryptographer, Malcolm J. Williamson, developed what is now known as Diffie–Hellman key exchange.

These discoveries were not publicly acknowledged for 27 years, until the research was declassified by the British government in 1997

Public Key Cryptography History IIA

From Wikipedia: Public Key Cryptography Public Discovery

1976: an asymmetric key cryptosystem was published by Whitfield Diffie and Martin Hellman who disclosed a method of public key agreement. This method of key exchange, which uses exponentiation in a finite field, came to be known as Diffie–Hellman key exchange. This was the first published practical method for establishing a shared secret-key over an authenticated (but not confidential) communications channel without using a prior shared secret.

Public Key Cryptography History IIB

From Wikipedia: Public Key Cryptography Public Discovery

1977: a generalization of Cocks’ scheme was independently invented by Ron Rivest, Adi Shamir and Leonard Adleman, all then at MIT. The latter authors published their work in 1978 in Martin Gardner’s Scientific American column, and the algorithm came to be known as RSA.

Asymmetric Cryptography Concepts

Two Keys: Public and Private

From Wikipedia: Public Key Cryptography

Sending a Message with a Public Key

From Wikipedia: Public Key Cryptography

Public Key Cryptography Properties

Very hard to determine private key from public key, i.e., like symmetric cryptography
Very hard to determine private key from messages, i.e., like symmetric cryptography
Can openly share public key so that others can send private message to you

How Many Keys do we need?

Only \(N\) Keys! No secure channel needed!

Public Key Families

RSA – based on properties of large prime numbers
Elliptic Curve – based on the “algebraic structure of elliptic curves over finite fields”, caution see SafeCurves
ElGamal – based on difficulty of computing discrete logarithms.

Python Hands On Pubic Key Encryption

RSA Algorithm Imports

Some Imports

from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives import serialization
from cryptography.hazmat.primitives.asymmetric import padding
from cryptography.hazmat.primitives import hashes

Alice’s Key Generation

See Python Cryptography RSA for recommended parameters

alice_private_key_rsa = rsa.generate_private_key(public_exponent=65537, key_size=2048)
alice_public_key_rsa = alice_private_key_rsa.public_key()

Bob’s Key Generation

See Python Cryptography RSA for recommended parameters

bob_private_key_rsa = rsa.generate_private_key(public_exponent=65537, key_size=2048)
bob_public_key_rsa = bob_private_key_rsa.public_key()

Set Padding Algorithm

See Python Cryptography RSA for recommended approach

myPad = padding.OAEP(mgf=padding.MGF1(algorithm=hashes.SHA256()), 
                     algorithm=hashes.SHA256(), label=None)

Alice Sends Message to Bob

Alice uses Bob’s public key to encrypt

message = b"Hi Bob, Alice here. I got your public key from trusted source. Just testing!"
bob_ciphertext = bob_public_key_rsa.encrypt(message, myPad)

Looking at the Ciphertext

def bytes2ascii(bs):
    # Printable ASCII is 32-126
    outstring = ""
    for b in bs:
        if b >= 32 and b <= 126:
            outstring += chr(b)
        else:
            outstring += "X"
    return outstring

Ciphertext for Bob

print(bytes2ascii(bob_ciphertext))
# XX%XX$XXl?+^XRVk9`aX?tXXXwWXIXX-XXyXX*XXXXXXX#M?XXXXXXXXXXXxX'XX)XZ&XXX)XWX2X|XeeXXXrXXX"XXXXYXX}wXX>XJXX(<XXXXX$XXvXXX(XXXX,XXXXGXXt7&X$!XdXXX XXXX@XX.XX ZoXlX8X3XfXX:X<XTXXXXGXwXcXbXX?XQ\XWXXoXDXXXXgXXXDXXXYXXZXHXXXXX$X3XXXXXilXX0IX\XXXXgXxXXOXXXXXX%@amX

Bob Deciphers the Message

Bob uses his private key to decrypt

plaintext = bob_private_key_rsa.decrypt(bob_ciphertext, myPad)
print(plaintext)

Key Exchange

Performance of Public Key Encryption

Nothing is Perfect

Public Key based Encryption is much slower than similarly secure symmetric algorithms
Hence public key algorithms are not directly used for bulk encryption
Instead they are used in key exchange, signing, and verification

Diffie-Hellman Key Exchange

Using public and private information securely come up with a common secret key for symmetric key cryptography algorithms such as AES. The algorithm takes advantage of the difficulty in computing discrete logarithms.

Diffie-Hellman Diagram

From Diffie-Hellman Key Exchange

Python Hands On Key Exchange

Diffie-Hellman
Elliptic Curve Key Exchange algorithm DH generalized to Elliptic Curves
X25519 key exchange, X448 key exchange: two specific elliptic curve DH key exchange algorithms.

Generation of Ed25519 Pairs

from cryptography.hazmat.primitives.asymmetric.x25519 import X25519PrivateKey

alice_private_key = X25519PrivateKey.generate()
alice_public_key = alice_private_key.public_key()

bob_private_key = X25519PrivateKey.generate()
bob_public_key = bob_private_key.public_key()

Alice Symmetric Key Generation

# Alice creates a symmetric key with her private key and Bob's public key
shared_key_alice = alice_private_key.exchange(bob_public_key)
print(shared_key_alice)

Bob Symmetric Key Generation

# Bob creates a symmetric key with her private key and Alice's public key
shared_key_bob = bob_private_key.exchange(alice_public_key)
print(shared_key_bob)

shared_key_alice == shared_key_bob

Man-in-the-middle (MITM) Attack

From NCyTE Applied Cryptography

Missing Pieces

Authenticity how do we know who really sent the message?
Integrity how do we know that the message hasn’t been modified?

Public Key Cryptography in the Real World Part I

What does TLS 1.3 Support?

From RFC8446

/* RSASSA-PKCS1-v1_5 algorithms */
rsa_pkcs1_sha256(0x0401),
rsa_pkcs1_sha384(0x0501),
rsa_pkcs1_sha512(0x0601),

/* ECDSA algorithms */
ecdsa_secp256r1_sha256(0x0403),
ecdsa_secp384r1_sha384(0x0503),
ecdsa_secp521r1_sha512(0x0603),

/* RSASSA-PSS algorithms with public key OID rsaEncryption */
rsa_pss_rsae_sha256(0x0804),
rsa_pss_rsae_sha384(0x0805),
rsa_pss_rsae_sha512(0x0806),

/* EdDSA algorithms */
ed25519(0x0807),
ed448(0x0808),

/* RSASSA-PSS algorithms with public key OID RSASSA-PSS */
rsa_pss_pss_sha256(0x0809),
rsa_pss_pss_sha384(0x080a),
rsa_pss_pss_sha512(0x080b),

SSH with No Password

How can we log into a remote server without always typing passwords?
Use public key cryptography!
Really? Yup. How do I do that?

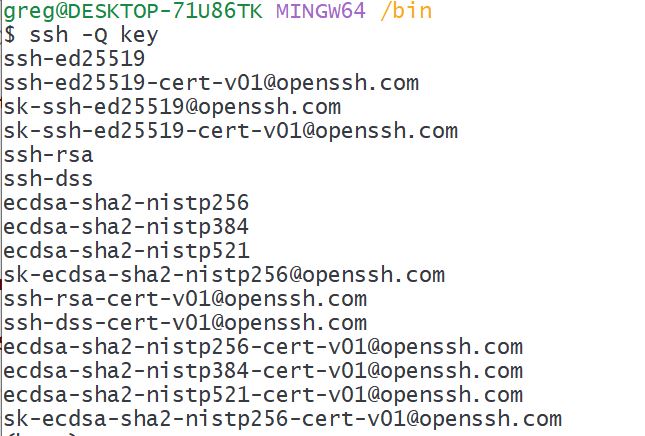
What does SSH Support

SSH References/Sites

OpenSSH – Open source SSH code
SSH.com information – Lot’s of helpful info
NIST:Security of Interactive and Automated Access Management Using Secure Shell (SSH)

SSH Key Generation I

See man page: ssh-keygen

Key options (-t): dsa, ecdsa, ecdsa-sk, ed25519, ed25519-sk, rsa
Out to file: -f filename
Usage example: ssh-keygen -f keyFile
Usage example: ssh-keygen -t ed25519 -f keyFile2

SSH Key Generation II

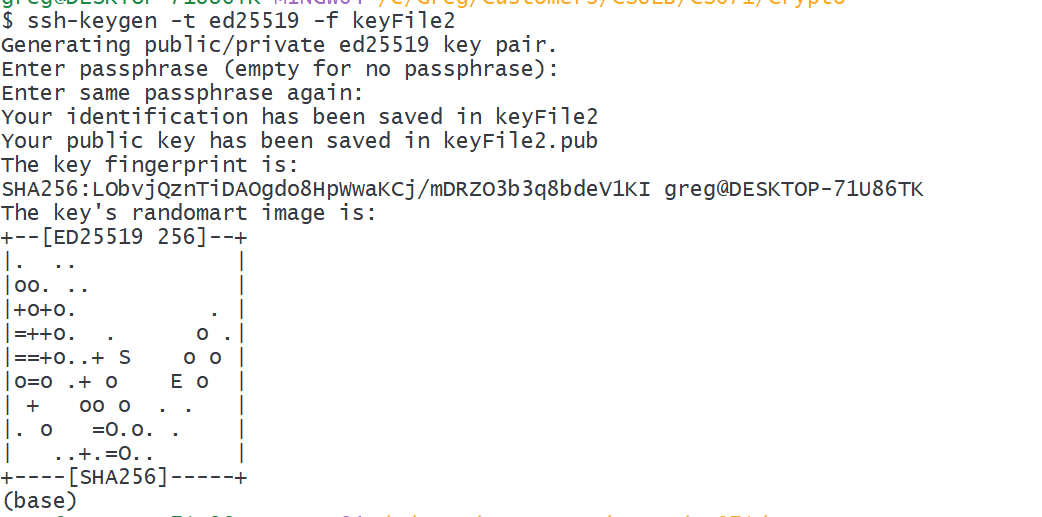
ssh-ed25519 AAAAC3NzaC1lZDI1NTE5AAAAIA5E8II0QJ/2Pd9Wjky8DMG+Xf9AQH61lITQkwLvBS1t greg@DESKTOP-71U86TK

Server SSH Files

From sshd the server can have an “authorized key file”

Default ~/.ssh/authorized_keys and ~/.ssh/authorized_keys2
Each line of the file contains one key (empty lines and lines starting with a ‘#’ are ignored as comments).
Public keys consist of the following space-separated fields: options, keytype, base64-encoded key, comment. The options field is optional.

Example authorized_keys file

ssh-rsa AAAAB3NzaC1yc2EAAAADAQABAAABAQC5X6gfWaQnc1PRKYC3t3U7dCEkN5wE+1HqnH6OwTtH0YMcvc3liILwp0qoao52NV1e3zRQiTeIWXa278UdSEiDmn9+VtFcZRNJYYlop5CuGOIvDt30vRrxeMNLI2Cg+zvcNOFaLxpnmJyajklScgnJwJj3qN6fCj6Wn6I+H8VYyBzRguaT3We0XSKZ5PzsW7tWRuFut/cBpMcbUWbgtBZvIGoU7LXnsNvDE+DLqAnEjeLJdBKRvjiLLHKcZVVS2j2Ua1U1mVFtNC0d2TO03LGqB4CNQhJ91y1n2TN8FS7764VbSjK1TFKNUJUN/1a+yU4BBNZWtHy8rxVw/Xx60VJJ gregb@DESKTOP-NOE6DKP

Add your Key to the Server

Manually add your public key that you generated on your machine to the authorized_keys file on the server.
Use the ssh-copy-id command to help you do this without the manual file editing.
Example use: ssh-copy-id -i keyFile2 greg@192.168.1.220