Readings

NCyTE: Applied Cryptography Module

1. Symmetric Key Cryptography Presentation
2. Public Key Cryptography Presentation
3. Hash Function Presentation
4. Digital Signatures Presentation

References

• Crypto101, for programmers, Python Cryptography Package for getting things done safely

• GnuPG – Gnu Privacy Guard, GPG4Win – Gnu Privacy Guard for Windows

• Cryptography: An Introduction(3rd Edition), Nigel Smart, free PDF from author, aimed at a rigorous undergraduate math course, 436 pages.

• An Introduction to Cryptography, Mohamed Barakat, Christian Eder, Timo Hanke, 2018, free PDF from authors, rigorous mathematical approach, 145 pages

Learning Objectives 1

From NCyTE

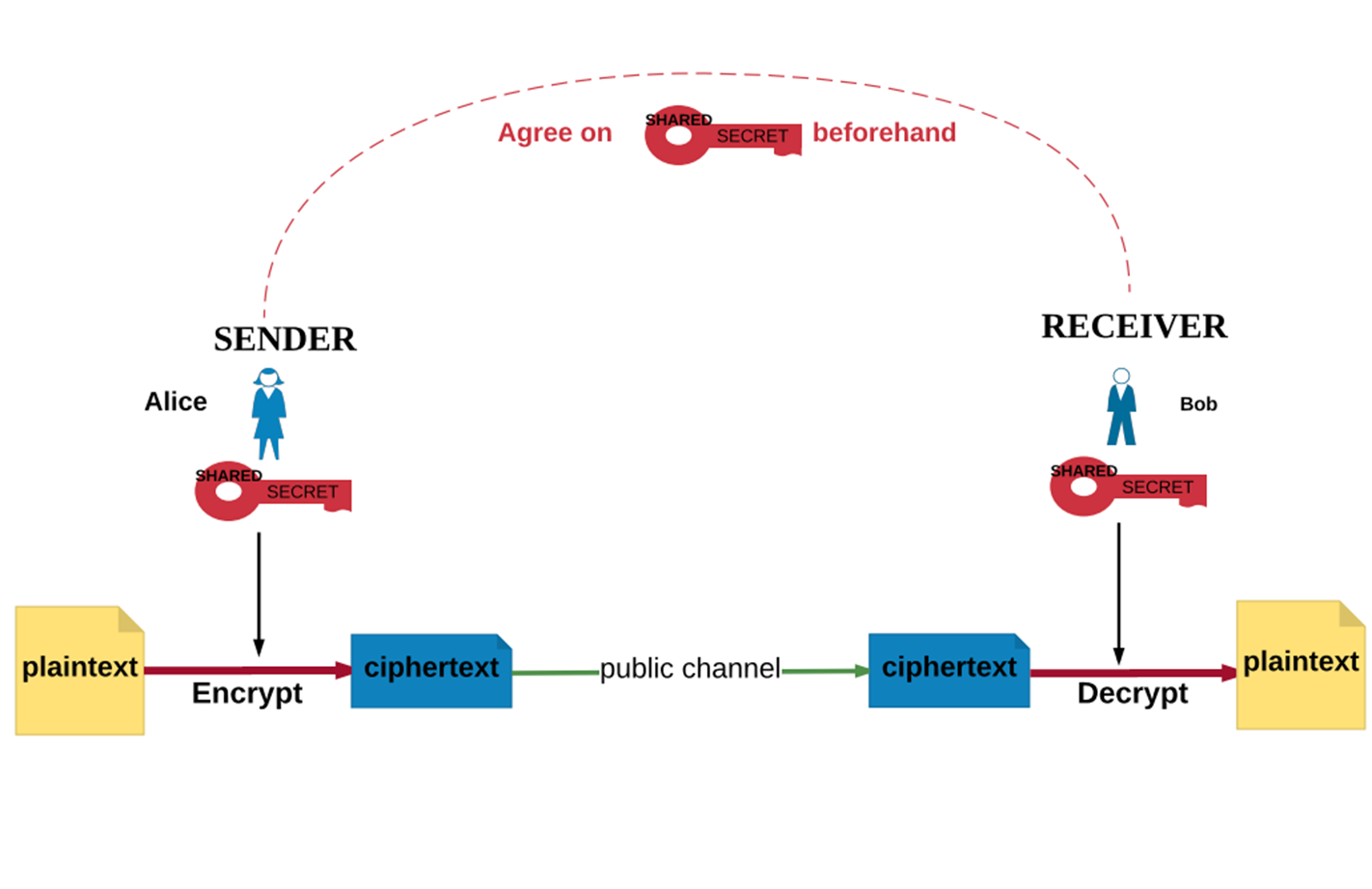
• Students will be able to define encryption, decryption, plaintext, ciphertext, and encryption/decryption key, and explain their use in cryptography.

• Students will be able to describe attack scenarios against an encryption algorithm.

• Students will be able to use early cipher methods such as a Caesar cipher or substitution cipher to encrypt/decrypt data “by hand”.

Learning Objectives 2

From NCyTE

• Students will be able to identify commonly used algorithms for symmetric encryption.

• Students will be able to explain the challenge of key distribution in symmetric key encryption.

Main Tenets of InfoSec

From NCyTE

• Confidentiality
• Integrity
• Availability
• Authenticity – How do we know where it came from
• Non-repudiation

Cryptography

From NCyTE

• Cryptography is “the practice and study of techniques for secure communication in the presence of adversaries” (Wikipedia)

• It is the science of designing systems to store and transmit data in a secure way so that it preserves its integrity and is accessible to only those with proper authentication and authorization.

Cryptography and the Main Tenets of InfoSec

From NCyTE

• Confidentiality: Encryption/decryption algorithms
• Integrity: Hash functions
• Authenticity: Digital signatures, digital certificates
• Non-repudiation: Digital signatures, digital certificates

Cryptology

From NCyTE

• Cryptanalysis: breaking cryptographic systems

• Cryptography

  • Symmetric Algorithms (symmetric key)
  • Asymmetric Algorithms (public key)

Symmetric Key Cryptography

From NCyTE

Key Components in Symmetric Key Crypto 1

• Plaintext: The message prior to encryption, after decryption
• Sender: traditionally referred to as Alice (A)
• Receiver: traditionally referred to as Bob (B)
• Ciphertext: The message after encryption

Key Components in Symmetric Key Crypto 2

• Key/Shared secret: Used in encryption/decryption
• Encrypt: algorithm to turn plaintext into ciphertext
• Decrypt: algorithm to turn ciphertext into plaintext

Definition

Map each letter to a letter further in the alphabet by a fixed amount

Python Implementation 1

Rotate a string or list of characters

alphaUpper = "ABCDEFGHIJKLMONPQRSTUVWXYZ"

def rotate(n, alist):
    """ Rotates a list/string by the integer n (less than the list length).
        Use this in the creation of Caesar/shift ciphers
    """
    return alist[n:] + alist[:n] # Python list slice trick

print(rotate(4, alphaUpper)) # try it

Python Implementation 2

Create a character “map” based on rotated string

def createCMap(permList):
    """Creates a cipher map for simple encryption.
    
    The permList is a permuted string/list of uppercase letters.
    Returns a dictionary that can be used to map characters
    """
    mapDict = {}
    for i, v in enumerate(alphaUpper):
        mapDict[v] = permList[i]
    return mapDict

cMapRot3 = createCMap(rotate(3, alphaUpper)) # try it
print(cMapRot3)
exLetter = "G"
print(f"The letter {exLetter} gets transformed into {cMapRot3[exLetter]}")

Python Implementation 3

Create function encrypt messages with cipher map

def encryptChars(plain, cipherMap):
    upMessage = plain.upper()
    cText = ""
    for char in upMessage:
        if char in alphaUpper: # Only encrypt uppercase characters
            cText += cipherMap[char]
        else:
            cText += char # leave spaces, puntuation, etc. alone
    return cText

# Try it       
ctext = encryptChars("Time to go Windsurfing", createCMap(rotate(6, alphaUpper)))
print(ctext)
# Decipher it
tempText = encryptChars(ctext, createCMap(rotate(20, alphaUpper)))
print(tempText)

Shift Cipher Examples

Challenge: decipher these messages!

• CSJSF, SJSF IGS N GVWTH QWDVSF!
• ESP ZPIE OLDP DEFNJ TD DSLNYH MCYVPCD
• IS TSY BWOYJ DSZW SBT HWDUYS FQLSWOYMR
• UTZ GRR GRMTXNZOSY GXK KWAGR!

Cryptanalysis of Shift Cipher

From NCyTE

Brute force approach: Try out all possible keys.

• What is the key space? How many keys are there?
  • For an English alphabet, there are 26. (Why?)
• Note that we assume here that the cryptanalyst knows the language that the original plaintext is in.

Brute Force Example 1

Encrypted message: OYP FEK KIP KYVD RCC? TEDGLKVIJ RIV WRJK.

ctext = "OYP FEK KIP KYVD RCC? TEDGLKVIJ RIV WRJK."
for i in range(0,26):
    text = encryptChars(ctext, createCMap(rotate(i, alphaUpper)))
    print(f"try {i+1} text: {text}")

Brute Force Example 2

Trying them all:

Kerckhoffs’s Principle

From NCyTE

• Auguste Kerckhoffs (1835-1903) Dutch linguist and cryptographer

• A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.

• Contrast “Security by obscurity” with Kerckhoffs’s Principle.

Open design Principle

Saltzer and Schroeder 1975, from CyBOK Intro

Cryptanalysis of a Cipher

Clearly state assumptions on what an attacker may have. Following Kerckhoffs’s Principle, we assume that the details of the algorithm used for encryption is known. Does the attacker have:

• Ciphertext?
• Pairs of plaintexts and ciphertexts?
• The ability to choose any plaintext (and obtain the corresponding ciphertext) without knowledge of the key?
• The ability to choose certain ciphertexts and get the corresponding plaintext without knowledge of the key?

Attack Scenarios on Ciphers

• Ciphertext only attacks: The attacker has only ciphertext(s).
• Known plaintext attacks: The attacker has ciphertext(s) and plaintext(s) for some of the ciphertexts.
• Chosen plaintext attacks: The attacker has ciphertexts and can choose a limited number of plaintexts and compute corresponding ciphertexts.
• Chosen ciphertext attacks: The attacker has the same ability as with chosen plaintext attacks, plus he/she can query a limited number of ciphertexts and get the plaintext for them.

System Model with Adversaries

From An Introduction to Cryptography:

Substitution Cipher Definition

• In this cipher, each letter/character in the plaintext alphabet is substituted by a different letter/character in the ciphertext alphabet.

• If the alphabet we are using for the plaintext and ciphertext are both letters in the English alphabet, then the substitution cipher substitutes each letter for a different letter. In this case, the key is a reordering of the letters in the alphabet.

• For example, the key ZYXWVUTSRQPONMLKJIHGFEDCBA would mean A is mapped to Z, B is mapped to Y, etc.

Substitution Cipher Visualization

Creating Random Substitutions with Python

We use the Python random standard library module

import random
alphaUpper = "ABCDEFGHIJKLMONPQRSTUVWXYZ"
randSub = random.sample(alphaUpper, len(alphaUpper))
print("".join(randSub)) # Join the list of characters into a string
randSub = random.sample(alphaUpper, len(alphaUpper))
print("".join(randSub)) # Join the list of characters into a string
randSub = random.sample(alphaUpper, len(alphaUpper))
print("".join(randSub)) # Join the list of characters into a string

Python Substitution Encryption

You use sherlockHolmes.txt or any text you like

randSub = random.sample(alphaUpper, len(alphaUpper))
# You can use any text that you want here
sherlock = open("sherlockHolmes.txt", "r", encoding="utf8")
book = sherlock.read()
cBook = encryptChars(book, createCMap(randSub))
print(cBook[690:1240])

A Encrypted Book

A book encrypted with our substitution cipher:

Brute force Attack on Substitution Cipher

• I will let you try this if you like…
• But how many permutations of 26 letters are there?
• Is 26! (26 factorial) a larger number?

Ciphertext only Attacks

Wikipedia: Letter Frequency

Compute the Letter Frequencies of the Ciphertext 1

def sortedFreqs(text):
    freqs = {} # Set up a dict to track letter counts
    for char in alphaUpper:
        freqs[char] = 0
    for char in text: # Got through the text
        upper = char.upper()
        if upper in alphaUpper: # only consider letters
            freqs[upper] += 1
    letters = list(freqs.items()) # get dictionary as tuples
    letters.sort(key=lambda x: -x[1]) # Sort based on frequency
    return letters

Compute the Letter Frequencies of the Ciphertext 2

cCommonFreqs = sortedFreqs(cBook)
print(cCommonFreqs)
cMostCommon = [x[0] for x in cCommonFreqs]
print("".join(cMostCommon))
print(mostCommon)
# [('Y', 54972), ('X', 40545), ('I', 36147), ('K', 34868), ('T', 31241), ('S', 29701), ('D', 29589), ('P', 27943), ('O', 25710), ('W', 19065), ('F', 17634), ('U', 13605), ('J', 12151), ('C', 11555), ('Z', 11119), ('H', 9777), ('A', 9363), ('N', 8313), ('M', 7240), ('G', 6646), ('Q', 4568), ('V', 3685), ('L', 579), ('E', 545), ('B', 438), ('R', 153)]
# YXIKTSDPOWFUJCZHANMGQVLEBR
# ETAOINSHRDLCUMWFGYPBVKJXQZ

Create the Inverse Substitution

def createDMap(sampFreq, actualFreq):
    """Creates a decipher map for simple decryption.
    
    sampFreq is a list/string of most frequent to least frequent letters seen in sample
    actualFreq is theoretical or known frequencies
    Returns a dictionary that can be used to decipher characters
    """
    mapDict = {}
    for i, v in enumerate(sampFreq):
        mapDict[v] = actualFreq[i]
    return mapDict

# Use it to decrypt
dMap1 = createDMap(cMostCommon, mostCommon)
dbook1 = encryptChars(cBook, dMap1)
print(dbook1[690:1240])

Decryption Result

What Went Wrong?

Compare Letter Frequency of Book to “Common”

# Check letter frequencies of the book
bookFreqs = sortedFreqs(book)
# Most frequent
bookCommon = [x[0] for x in bookFreqs]
print("".join(bookCommon))
print(mostCommon)
# ETAOINHSRDLUMWCYFGPBVKXJQZ
# ETAOINSHRDLCUMWFGYPBVKJXQZ

Known Plaintext Attack

If we knew what book was being sent we would know the exact letter frequencies and use those to create our inverse substitution.

dMap2 = createDMap(cMostCommon, bookCommon)
dbook2 = encryptChars(cBook, dMap2) 
print(dbook2[690:1240])

Known Plaintext Attack Result

Chosen Plaintext Attack

Can we make our life easier with “special” plaintext?

special = ""
for i, v in enumerate(alphaUpper):
    special += (i+1)*v
print(special)
# ABBCCCDDDDEEEEEFFFFFFGGGGGGGHHHHHHHHIIIIIIIIIJJJJJJJJJJKKKKKKKKKKKLLLLLLLLLLLLMMMMMMMMMMMMMOOOOOOOOOOOOOONNNNNNNNNNNNNNNPPPPPPPPPPPPPPPPQQQQQQQQQQQQQQQQQRRRRRRRRRRRRRRRRRRSSSSSSSSSSSSSSSSSSSTTTTTTTTTTTTTTTTTTTTUUUUUUUUUUUUUUUUUUUUUVVVVVVVVVVVVVVVVVVVVVVWWWWWWWWWWWWWWWWWWWWWWWXXXXXXXXXXXXXXXXXXXXXXXXYYYYYYYYYYYYYYYYYYYYYYYYYZZZZZZZZZZZZZZZZZZZZZZZZZZ

Easy Frequency Analysis 1

Do you see another pattern here?

randSub2 = random.sample(alphaUpper, len(alphaUpper)) # New substitution
secretStuff = encryptChars("Do not ever use this cipher in real life!", createCMap(randSub2))
print(secretStuff)
ctextSpecial = encryptChars(special, createCMap(randSub2))
print(ctextSpecial)

Easy Frequency Analysis 2

Try it!

specialFreqs = sortedFreqs(special)
cSpecialFreqs = sortedFreqs(ctextSpecial)
dMapSpecial = createDMap([x[0] for x in cSpecialFreqs], [x[0] for x in specialFreqs])
print(dMapSpecial)
print(encryptChars(secretStuff, dMapSpecial))

Take Aways

• A Large key space doesn’t guarantee security
• Crypto algorithms are subject to a wide variety of attacks
• Only use well proven algorithms